|
Wednesday, October 2, 2013
Print a Line with Empty Main()
Sunday, September 29, 2013
Thursday, September 26, 2013
Permutation of a given String.
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
int main()
{
string s;
cin>>s;
cout<<"\n Permutations Are\n";
do
{
cout<<s<<"\n";
}while(next_permutation(s.begin(),s.end()));
return 0;
}
Permutation of a Given Values.
Q. Let given values are 1,2,3.
The permutations are
123
132
213
231
312
321
Source Code is:-
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int main()
{
vector<char> v;
int n;
char num;
cout<<"\n Emter N::";
cin>>n;
cout<<"\n Enter Elements:";
for(int i=0;i<n;i++)
{
cin>>num;
v.push_back(num);
}
cout<<"\n Elements Are::";
for(int i=0;i<v.size();i++)
cout<<" "<<v[i];
cout<<"\n Permutations Are\n";
do
{
for(int i=0;i<v.size();i++)
{ if(i%5==0)
cout<<"\n";
cout<<" "<<v[i];
}
cout<<"\t";
}while(next_permutation(v.begin(),v.end()));
return 0;
}
The permutations are
123
132
213
231
312
321
Source Code is:-
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int main()
{
vector<char> v;
int n;
char num;
cout<<"\n Emter N::";
cin>>n;
cout<<"\n Enter Elements:";
for(int i=0;i<n;i++)
{
cin>>num;
v.push_back(num);
}
cout<<"\n Elements Are::";
for(int i=0;i<v.size();i++)
cout<<" "<<v[i];
cout<<"\n Permutations Are\n";
do
{
for(int i=0;i<v.size();i++)
{ if(i%5==0)
cout<<"\n";
cout<<" "<<v[i];
}
cout<<"\t";
}while(next_permutation(v.begin(),v.end()));
return 0;
}
Compress a String.
Ques. How to compress string in the given format?
Write a function that takes as input a string such as "aabbccdef" and outputs a2b2c2def" or "a4bd2g4" for "aaaabddgggg".
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{ int c;
string s,temp;
cin>>s;
sort(s.begin(),s.end());
for(int i=0;i<s.length();++i)
{if(s[i]!=s[i+1])
{
c=count(s.begin(),s.end(),s[i]);
cout<<s[i];
if(c>1)
{cout<<c;}
}
}
return 0;
}
Write a function that takes as input a string such as "aabbccdef" and outputs a2b2c2def" or "a4bd2g4" for "aaaabddgggg".
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{ int c;
string s,temp;
cin>>s;
sort(s.begin(),s.end());
for(int i=0;i<s.length();++i)
{if(s[i]!=s[i+1])
{
c=count(s.begin(),s.end(),s[i]);
cout<<s[i];
if(c>1)
{cout<<c;}
}
}
return 0;
}
Sunday, September 22, 2013
Shortest Program to perform operation of Singly Linked List.
#include <iostream>
#include <list>
#include<stdlib.h>
using namespace std;
int main ()
{
std::list<int> l;
std::list<int>::iterator it;
do
{int c,d,n,pos;
cout<<"\n\t\t Single Linked List Operations. \n 1.Insert \t 2.Delete \t 3.Display \t4.Exit.\n\n Enter Your Choice:";cin>>c;
switch(c)
{case 1: cout<<"\n\t Insert Operations\n\t 1.Begining \t 2.End \t 3.At a given position\nEnter your choice:";cin>>d;
switch(d)
{case 1:cout<<"\n Enter Element::";cin>>n;l.push_front(n);break;case 2:cout<<"\n Enter Element::";cin>>n;l.push_back(n);break;
case 3:cout<<"\n Enter Element::";cin>>n;cout<<"\n Enter Position:";cin>>pos;it = l.begin();for(int i=0;i<pos-1;i++)++it;l.insert(it,n);break;
default:cout<<"\n Wrong Choice.!!!";break;
}break;
case 2:if(l.size()==0){cout<<"\nEmpty List.";break;}else{cout<<"\n Enter Position::";cin>>pos;it = l.begin();for(int i=0;i<pos-1;i++)++it;l.erase(it);break;}
case 3:if(l.size()==0){cout<<"\nEmpty List.";break;}else{for (it=l.begin(); it!=l.end(); ++it)std::cout << ' ' << *it<<"\n";break;}
case 4:exit(1);break;
default:cout<<"Wrong Choice!!!!\n";break;}
}while(1);
return 0;
}
Shortest Program to perform Stack Operations Using () Header File.
**This program may not run on Older Versions of GCC. Use 4.8.1 GCC Compiler to run this program.
#include<iostream>
#include<stack>
#include<cstdlib>
using namespace std;
int main()
{
stack<int> s;
int ch,n;
cout<<"\n \t\t STACK OPERATIONS \n\n 1.PUSH \t2.POP\t 3.DISPLAY\t4.EXIT.\n\n Enter Your Choice::";
cin>>ch;
switch(ch)
{
case 1:cout<<"\n Element::";cin>>n;s.emplace(n);main();break;
case 2:s.pop();main();break;
case 3:for(int i=0;i<s.size();i++)
cout<<"\n"<<s.top();
main();break;
case 4:exit(0);
default:cout<<"\n\t\n Wrong Choice !!";
main();break;
}
return 0;
}
Wap to perform Single Linked List Operations.
#include<stdio.h>
#include<stdlib.h>
struct node
{
int info;
struct node *link;
};
struct node *start;
int ins_beg()
{
struct node *new_node;
new_node=(struct node*)malloc(sizeof(struct node));
printf("\n Enter the element:");
scanf("%i",&new_node->info);
if(start==NULL)
{
new_node->link=NULL;
start=new_node;
}
else
{
new_node->link=start;
start=new_node;
}
printf("\n Element Inserted sucessfully.\n");
main();
}
int ins_end()
{
struct node *new_node,*lp;
new_node=(struct node*)malloc(sizeof(struct node));
printf("\n Enter the element:");
scanf("%i",&new_node->info);
if(start==NULL)
{
new_node->link=NULL;
start=new_node;
}
else
{
lp=start;
while(lp->link!=NULL)
{
lp=lp->link;
}
lp->link=new_node;
new_node->link=NULL;
}
printf("\n Element Inserted sucessfully.\n");
main();
}
int ins_pos()
{
struct node *new_node,*tptr;
int pos,i=0;
printf("\n Enter the position:");
scanf("%i",&pos);
if(pos==1)
{ins_beg();
main();}
else
{
tptr=start;
for(i=1;i<(pos-1)&&tptr!=NULL;i++)
tptr=tptr->link;
if(tptr==NULL)
{printf("\n Invalid Position.");
main();}
else
{ new_node=(struct node*)malloc(sizeof(struct node));
printf("\n Enter the element:");
scanf("%i",&new_node->info);
new_node->link=tptr->link;
tptr->link=new_node;
printf("\n Item Inserted Sucessfully.");
main();
}
}
main();
}
int disp()
{
struct node *t;
if(start==NULL)
{
printf("\n List is empty.");
return;
}
t=start;
printf("\n Elements are:");
while(t!=NULL)
{
printf("\n\n%i",t->info);
t=t->link;
}
main();
}
int del()
{
int pos;
struct node *tptr,*ptr;
ptr=start;
printf("\n Enter the Position::");
scanf("%d",&pos);
if(pos==1)
{
start=start->link;
}
else
{ int i=0;
while(i<pos-1 && ptr!=NULL)
{
tptr=ptr;
ptr=ptr->link;
i++;
}
tptr->link=ptr->link;
}
main();
}
int main()
{
do
{
int c,d;
printf("\n\t\t Single Linked List Operations. \n 1.Insert \t 2.Delete \t 3.Display \t4.Exit.\n\n Enter Your Choice:");
scanf("%d",&c);
switch(c)
{
case 1:printf("\n\t Insert Operations\n\t 1.Begining \t 2.End \t 3.At a given position\nEnter your choice:");
scanf("%d",&d);
switch(d)
{
case 1:ins_beg();break;case 2:ins_end();break;case 3:ins_pos();break;default:printf("\n Wrong Choice.!!!");main();break;
}
case 2:del();break;
case 3:disp();break;
case 4:exit(1);break;
default:printf("Wrong Choice!!!!\n");break;
}
}while(1);
return 0;
}
Thursday, September 19, 2013
Wap to compute the area of a isosceles triangle.
#include<stdio.h>
#include<math.h>
int main() {
int a, b, c;
float area, s;
printf("Enter the sides of a triangle:\n");
scanf("%d%d%d", &a, &b, &c);
if ((a + b > c && a + c > b && b + c > a) && (a > 0 && b > 0 && c > 0)) {
if (a == b || b == c || a == c) {
s = (a + b + c) / 2.0;
area = sqrt((s * (s - a) * (s - b) * (s - c)));
printf("\nArea of an isosceles triangle is: %2f\n", area);
} else {
printf("\nTriangle is not an isosceles ");
}
} else {
printf("\n Triangle formation not possible\n");
}
return 0;
}
WAP to classify the triangle as equilateral, isosceles and scalene.
#include<stdio.h>
#include<math.h>
int main() {
int a, b, c;
float s, area;
printf("Enter the values of the sides of the triangle: \n");
scanf("%d %d %d", &a, &b, &c);
if ((a + b > c && a + c > b && b + c > a) && (a > 0 && b > 0 && c > 0))
{
s = (a + b + c) / 2.0;
area = sqrt((s * (s - a) * (s - b) * (s - c)));
if (a == b && b == c)
{
printf("Equilateral Triangle. \n");
printf("Area of Equilateral Triangle is: %f", area);
}
else if (a == b || b == c || a == c)
{
printf("Isosceles Triangle. \n");
printf("Area of an Isosceles Triangle: %f", area);
}
else
{
printf("Scalene Triangle. \n");
printf("Area of Scalene Triangle: %f", area);
}
}
else {
printf("Triangle formation not possible");
}
return 0;
}
Print Your Name without using semicolon in program in C/C++
C
#include<stdio.h>
int main()
{
if(printf("Your Name"))
}
C++
#include<iostream>
using namespace std;
int main()
{
if(cout<<"Your Name")
return 0;
}
#include<stdio.h>
int main()
{
if(printf("Your Name"))
}
C++
#include<iostream>
using namespace std;
int main()
{
if(cout<<"Your Name")
return 0;
}
Infix to Post fix Conversion
#define SIZE 50 /* Size of Stack */
#include <ctype.h>
char s[SIZE];
int top = -1; /* Global declarations */
push(char elem) { /* Function for PUSH operation */
s[++top] = elem;
}
char pop() { /* Function for POP operation */
return (s[top--]);
}
int pr(char elem) { /* Function for precedence */
switch (elem) {
case '#':
return 0;
case '(':
return 1;
case '+':
case '-':
return 2;
case '*':
case '/':
return 3;
}
}
main() { /* Main Program */
char infx[50], pofx[50], ch, elem;
int i = 0, k = 0;
printf("\n\nRead the Infix Expression ? ");
scanf("%s", infx);
push('#');
while ((ch = infx[i++]) != '\0') {
if (ch == '(')
push(ch);
else if (isalnum(ch))
pofx[k++] = ch;
else if (ch == ')') {
while (s[top] != '(')
pofx[k++] = pop();
elem = pop(); /* Remove ( */
} else { /* Operator */
while (pr(s[top]) >= pr(ch))
pofx[k++] = pop();
push(ch);
}
}
while (s[top] != '#') /* Pop from stack till empty */
pofx[k++] = pop();
pofx[k] = '\0'; /* Make pofx as valid string */
printf("\n\nGiven Infix Expn: %s Postfix Expn: %s\n", infx, pofx);
}
Stack Operations.
#include<stdio.h>
#include<stdlib.h>
#define SIZE 10
int item,i;
int push(int stack[SIZE],int &tos,int item)
{
if(tos==SIZE-1)
{printf("\n Stack Overflow.");
}
tos=tos+1;
stack[tos]=item;
return 0;
}
int pop(int stack[SIZE],int &tos)
{
int no;
if(tos==-1)
printf("\n Stack is empty Cannot delete any Element...\n");
else
{no=stack[tos];
tos=tos-1;}
return 0;
}
int display(int stack[SIZE],int tos)
{ if(tos==-1)
printf("\n Stack Is Empty......\n");
else{
printf("\n Stack is:\n");
for(i=tos;i>=0;i--)
{ printf("\n __\n|");
printf("%d",stack[i]);
printf("|");}}
}
int main()
{
int ch,stack[SIZE],n;
static int tos=-1;
do
{
printf(" \n STACK OPERATIONS \n\t1.FILL STACK(before pushing) 2.PUSH\t 3.POP\t4.DISPLAY\t5.EXIT\n");
scanf("%d",&ch);
switch(ch)
{ case 1:printf("\n Enter the no of elements to be inserted:");
scanf("%d",&n);
printf("\n Enter elements:");
for(i=0;i<n;i++)
{scanf("%d",&stack[i]);tos++;}
break;
case 2:
printf("\n Enter the element to be inserted:");
scanf("%d",&item);
push(stack,tos,item);
break;
case 3:
pop(stack,tos);
break;
case 4:display(stack,tos);
break;
case 5:printf("\n Terminating......");
exit(0);
break;
default:printf("\n Wrong Choice!!!");
break;
}printf("\n Press Any Key to Continue.......\n ");
}while(n!=5);
return 0;
}
Wednesday, September 18, 2013
Program to find the transitive closure of a matrix using Warshall's Algorithm.
#include<stdio.h>
int i,j;
#define V 4
void transitiveClosure(int graph[V][V])
{
int i, j, k;
for (k = 0; k < V; k++)
{
for (i = 0; i < V; i++)
{
for (j = 0; j < V; j++)
{
graph[i][j] = graph[i][j] || (graph[i][k] && graph[k][j]);
}
}
}
printf ("Following matrix is transitive closure of the given graph\n");
for ( i = 0; i < V; i++)
{
for ( j = 0; j < V; j++)
printf ("%d ", graph[i][j]);
printf("\n");
}
}
int main()
{
int graph[V][V] = { {1, 1, 0, 1},
{0, 1, 1, 0},
{0, 0, 1, 1},
{0, 0, 0, 1}
};
transitiveClosure(graph);
return 0;
}
Program to print the Union And Intersection of a Program.
#include<stdio.h>
void Union(int set1[10],int set2[10],int m,int n);
void Intersection(int set1[10],int set2[10],int m,int n);
int main()
{
int a[10],b[10],m,n,i,j;
int ch;
printf("\nEnter the number of elements in first set:\n");
scanf("%d",&m);
printf("\nEnter the elements:\n");
for(i=0;i<m;i++)
{
scanf("%d",&a[i]);
}
printf("\nElement of First set:\n\n");
for(i=0;i<m;i++)
{
printf("%d\t",a[i]);
}
printf("\nEnter the number of elements in second set:\n");
scanf("%d",&n);
printf("\nEnter the elements:\n");
for(i=0;i<n;i++)
{
scanf("%d",&b[i]);
}
printf("\nElement of second set\n");
for(i=0;i<n;i++)
{
printf("%d\t",b[i]);
}
for(;;)
{
printf("\n\nMenu\n\n1.Union\n2.Intersection");
printf("\n3.exit");
printf("\nEnter your choice:\n");
scanf("%d",&ch);
switch(ch) {
case 1:
Union(a,b,m,n);
break;
case 2:
Intersection(a,b,m,n);
break;
case 3:
exit(0);
}
getch();
}
}
void Union(int a[10],int b[10],int m,int n)
{
int c[20],i,j,k=0,flag=0;
for(i=0;i<m;i++)
{
c[k]=a[i];
k++;
}
for(i=0;i<n;i++)
{
flag=0;
for(j=0;j<m;j++)
{
if(b[i]==c[j])
{
flag=1;
break;
}
}
if(flag==0)
{
c[k]=b[i];
k++;
}
}
printf("\nElement of resultant set\n\n");
for(i=0;i<k;i++)
{
printf("\t%d",c[i]);
}
}
void Intersection(int a[10],int b[10],int m,int n)
{
int c[20],i,j,k=0,flag=0;
for(i=0;i<m;i++)
{
flag=0;
for(j=0;j<n;j++)
{
if(a[i]==b[j])
{
c[k]=a[i];
k++;
}
if(k==0)
{
printf("\n\nResultant set is null set!\n");
}else{
printf("\nElement of resultant set\n");
for(i=0;i<k;i++)
{
printf("\t%d",c[i]);
}
Count Number of Digits in N! factorial.
#include<stdio.h>
#include<math.h>
double count_digit(long a)
{
double sum; long i;
if(a==0) return 1;
else
{
sum=0;
for(i=1;i<=a;i++)
sum+=log10(i);
return floor(sum)+1;
}
}
int main()
{
double sum; long n;
clrscr();
while(scanf("%ld",&n)==1)
{
sum = count_digit(n);
printf("%.0lf\n",sum);
}
getch();
}
Printing all possible subsets using Bit Mask
#include<stdio.h>
void PrintAllSubset(int n)
{
int mask,pos,i,j,no = 1<<n;
for(i=1;i<no;i++)
{
for(j=0;j<n;j++)
if((i&(1<<j)) > 0)
printf("%d ",j+1);
printf("\n");
}
}
int main()
{
int n;
while(scanf("%d",&n) == 1)
{
PrintAllSubset(n);
}
return 0;
}
Write a shortest program in C++ to sort a given array.
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
int n;
cin>>n;
int arr[n];
std::cout<<"\n Enter n elements in any order:";
for(int i=0;i<n;i++)
std::cin>>arr[i];
std::sort(arr,arr+n);
for(int i=0;i<n;i++)
std::cout<<arr[i]<<" ";
return 0;
}
Writing a Simple Program in C++ 4.3.2.
In Turbo C++ , we write a simple program as follows:-
#include<iostream.h>
#include<conio.h>
void main()
{clrscr();
int a;
cin>>a;
cout<<a;
getch();
}
But in latest C++ 4.3.2 Edition ,program is written as :-
#include<iostream>
using namespace std;
int main()
{
int a;
std::cin>>a;
std::cout<<a;
return 0;
}
#include<iostream.h>
#include<conio.h>
void main()
{clrscr();
int a;
cin>>a;
cout<<a;
getch();
}
But in latest C++ 4.3.2 Edition ,program is written as :-
#include<iostream>
using namespace std;
int main()
{
int a;
std::cin>>a;
std::cout<<a;
return 0;
}
- It is necessary to add using namespace std; in the beginning of the program.
- (.h) is not written after a header file name.
- <conio.h>,<graphics.h> etc. are omitted header files in C++.
- A main function should return a value.
Or simply program could be written as:-
#include<iostream>
using namespace std;
int main()
{
int a;
cin>>a;
cout<<a;
return 0;
}
using namespace std;
int main()
{
int a;
cin>>a;
cout<<a;
return 0;
}
Input by Fastest Method
Header File:-#include<cstdio> (For c++)
#include<wchar.h> (For C)
Input for Character Variables :-
Use getchar_unlocked() for fastest input.
Eg.
char ch;
ch=getchar_unlocked();
Input for Integer Variables :-
Define a function that will take the input as:-
#define get getchar_unlocked
inline int fastinput( )
{
int n = 0 , s = 1 ; char p = get( ) ;
if( p == '-' ) s=-1;
while( ( p < '0' || p > '9' ) && p != EOF && p != '-' )
p = get( ) ;
if( p == '-' )
s = -1 , p = get( ) ;
while( p >= '0' && p <= '9' )
{
n = ( n << 3 ) + ( n << 1 ) + ( p - '0' ) ;
p = get( ) ;
}
return n * s ;
}
Wednesday, August 28, 2013
GCD and LCM Using Euclid's Algorithm
GCD LCM Using Euclids Algorithm
#include <conio.h>
void main()
{
int num1, num2, gcd, lcm, remainder, numerator, denominator;
clrscr();
printf("Enter two numbers\n");
scanf("%d %d", &num1,&num2);
if (num1 > num2)
{
numerator = num1;
denominator = num2;
}
else
{
numerator = num2;
denominator = num1;
}
remainder = num1 % num2;
while(remainder !=0)
{
numerator = denominator;
denominator = remainder;
remainder = numerator % denominator;
}
gcd = denominator;
lcm = num1 * num2 / gcd;
printf("GCD of %d and %d = %d \n", num1,num2,gcd);
printf("LCM of %d and %d = %d \n", num1,num2,lcm);
}
Add without Add Operator
Add without ADD Operator
int main()
{
int a,b;
int sum;
printf("Enter any two integers: ");
scanf("%d%d",&a,&b);
//sum = a - (-b);
sum = a - ~b -1;
printf("Sum of two integers:%d",sum);
return 0;
}
Subtract Without Using Subtract Operator
Subtract without subtract operator
int main()
{
int a,b;
int sum;
printf("Enter any two integers: ");
scanf("%d%d",&a,&b);
sum = a + ~b + 1;
printf("Difference of two integers: %d",sum);
return 0;
}
Swap using Bitwise Operator
Swap two numbers using bitwise operators
int main()
{
int i = 65;
int k = 120;
printf("\n value of i=%d k=%d before swapping", i, k);
i = i ^ k;
k = i ^ k;
i = i ^ k;
printf("\n value of i=%d k=%d after swapping", i, k);
return 0;
}
Swap without using third variable
Swap Without using third variable
void main()
{
int a,b;
printf("Enter number1: ie a");
scanf("%d",&a);
printf("Enter number2:ie b ");
scanf("%d",&b);
printf(value of a and b before swapping is a=%d,b=%d"a,b);
a=a+b;
b=a-b;
a=a-b;
printf("value of a and b after swapping is a=%d,b=%d"a,b);
}
Sieve of Eratosthenes For Generating Prime Numbers
An algorithm for making tables of primes. Sequentially write down the integers from 2 to the highest number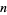 
you wish to include in the table. Cross out all numbers 
which are divisible by 2 (every second number). Find the smallest remaining number 
. It is 3. So cross out all numbers 
which are divisible by 3 (every third number). Find the smallest remaining number 
. It is 5. So cross out all numbers 
which are divisible by 5 (every fifth number).
you wish to include in the table. Cross out all numbers 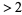which are divisible by 2 (every second number). Find the smallest remaining number 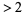. It is 3. So cross out all numbers 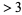which are divisible by 3 (every third number). Find the smallest remaining number 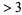. It is 5. So cross out all numbers 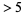which are divisible by 5 (every fifth number).
Continue until you have crossed out all numbers divisible by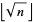 
, where 
is the floor function. The numbers remaining are prime. This procedure is illustrated in the above diagram which sieves up to 50, and therefore crosses out composite numbers up to 
. If the procedure is then continued up to 
, then the number of cross-outs gives the number of distinct prime factors of each number.
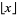, where is the floor function. The numbers remaining are prime. This procedure is illustrated in the above diagram which sieves up to 50, and therefore crosses out composite numbers up to 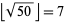. If the procedure is then continued up to 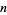, then the number of cross-outs gives the number of distinct prime factors of each number.
The sieve of Eratosthenes can be used to compute the prime counting function as
 |
which is essentially an application of the inclusion-exclusion principle.
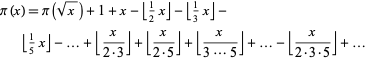Euclid's GCD Algorithm
One of the earliest known numerical algorithms is that developed by Euclid (the father of geometry) in about 300 B.C. for computing the greatest common divisor (GCD) of two positive integers.
Let GCD(x,y) be the GCD of positive integers x and y. If x = y, then obviously
.
Euclid's insight was to observe that, if x > y, then
.
Actually, this is easy to prove. Suppose that d is a divisor of both x and y. Then there exist integers q1 and q2 such that x = q1d and y = q2d. But then
x - y = q1d - q2d = (q1 - q2)d. Therefore d is also a divisor of x-y.
Using similar reasoning, one can show the converse, i.e., that any divisor of x-y and y is also a divisor of x. Hence, the set of common divisors of x and y is the same as the set of common divisors of x-y and y. In particular, the largest values in these two sets are the same, which is to say that GCD(x,y) = GCD(x-y,y).
A Java method that implements Euclid's algorithm is as follows:
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k != m) {
if (k > m)
{ k = k-m; }
else
{ m = m-k; }
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,k) = k
return k;
}
As an example, suppose that we use this method to compute the GCD of 420 and 96. If we were to take a snapshot of the method's local variables immediately before the first loop iteration and immediately after each iteration, we'd get
When k m -------------------- ----- ----- Before 1st iteration 420 96 After 1st iteration 324 96 After 2nd iteration 228 96 After 3rd iteration 132 96 After 4th iteration 36 96 After 5th iteration 36 60 After 6th iteration 36 24 After 7th iteration 12 24 After 8th iteration 12 12
A significant improvement in performance (in some cases) is possible, however, by using the remainder operator (%) rather than subtraction. Notice in the above that we subtracted m's value from k's four times before kbecame less than m. The same effect results from replacing k's value by k % m. (In this case, 420 % 96 is 36.) Using this approach forces us to change the loop condition, however, as here what will eventually happen is that one of k or m will become zero. (Indeed, k == m is impossible to arrive at unless K == M.) Note that GCD(x,0) = GCD(0,x) = x. (After all, x's greatest divisor is itself, which is also a divisor of zero.)
Our new method is as follows:
int gcd(int K, int M) {
int k = K; // In order to state a simple, elegant loop invariant,
int m = M; // we keep the formal arguments constant and use
// local variables to do the calculations.
// loop invariant: GCD(K,M) = GCD(k,m)
while (k !=0 && m != 0) {
if (k > m)
{ k = k % m; }
else
{ m = m % k; }
}
// At this point, GCD(K,M) = GCD(k,m) = max(k,m)
return Math.max(k,m);
}
Using this version of the method, we get the following snapshots:
When k m -------------------- ----- ----- Before 1st iteration 420 96 After 1th iteration 36 96 After 2nd iteration 36 24 After 3rd iteration 12 24 After 4th iteration 12 0
Notice that the number of loop iterations has been cut in half. Further code-simplification improvements are possible, however, by ensuring that k ≥ m. We can achieve this by replacing, on each iteration, k's value by m's and m's by k % m. This way, no if statement is needed:
int gcd(int K, int M) {
int k = Math.max(K,M);
int m = Math.min(K,M);
// loop invariant: k ≥ m ∧ GCD(K,M) = GCD(k,m)
while (m != 0) {
int r = k % m;
k = m;
m = r;
}
// At this point, GCD(K,M) = GCD(k,m) = GCD(k,0) = k
return k;
}
Using this version of the method, we get the following snapshots:
When k m -------------------- ----- ----- Before 1st iteration 420 96 After 1th iteration 96 36 After 2nd iteration 36 24 After 3rd iteration 24 12 After 4th iteration 12 0
Backtracking
Backtracking Algorithms
Solution Spaces
Backtracking is a refinement of the brute force approach, which systematically searches for a solution to a problem among all available options. It does so by assuming that the solutions are represented by vectors (v1, ..., vm) of values and by traversing, in a depth first manner, the domains of the vectors until the solutions are found.When invoked, the algorithm starts with an empty vector. At each stage it extends the partial vector with a new value. Upon reaching a partial vector (v1, ..., vi) which can’t represent a partial solution, the algorithm backtracks by removing the trailing value from the vector, and then proceeds by trying to extend the vector with alternative values.ALGORITHM try(v1,...,vi) IF (v1,...,vi) is a solution THEN RETURN (v1,...,vi) FOR each v DO IF (v1,...,vi,v) is acceptable vector THEN sol = try(v1,...,vi,v) IF sol != () THEN RETURN sol END END RETURN ()If Si is the domain of vi, then S1 × ... × Sm is the solution space of the problem. The validity criteria used in checking for acceptable vectors determines what portion of that space needs to be searched, and so it also determines the resources required by the algorithm.The traversal of the solution space can be represented by a depth-first traversal of a tree. The tree itself is rarely entirely stored by the algorithm in discourse; instead just a path toward a root is stored, to enable the backtracking.Traveling Salesperson
The problem assumes a set of n cities, and a salesperson which needs to visit each city exactly once and return to the base city at the end. The solution should provide a route of minimal length.The route (a, b, d, c) is the shortest one for the following one, and its length is 51.The traveling salesperson problem is an NP-hard problem, and so no polynomial time algorithm is available for it. Given an instance G = (V, E) the backtracking algorithm may search for a vector of cities (v1, ..., v|V |) which represents the best route.The validity criteria may just check for number of cities in of the routes, pruning out routes longer than |V |. In such a case, the algorithm needs to investigate |V ||V | vectors from the solution space.On the other hand, the validity criteria may check for repetition of cities, in which case the number of vectors reduces to |V |!.The Queens Problem
Consider a n by n chess board, and the problem of placing n queens on the board without the queens threatening one another.The solution space is {1, 2, 3,, n}n. The backtracking algorithm may record the columns where the different queens are positioned. Trying all vectors (p1, ..., pn) implies nn cases. Noticing that all the queens must reside in different columns reduces the number of cases to n!.
For the latter case, the root of the traversal tree has degree n, the children have degree n - 1, the grand children degree n - 2, and so forth.Checking for threatening positions along the way my further reduce the number of visited configurations.Convex Hull (Graham’s Scan)
The problem asks to construct the shortest polygon which encloses a given set of points on a plan. Intuitively, the polygon can be determined by placing a rubber around the set.Determine an extreme point with the largest x coordinate. Sort the points in order of increasing angles, relatively to the extreme point.Traverse the points in the sorted order, adding them to the partial solution upon making a turn of less than 180 degrees, and backtracking when making a larger turn.
The algorithm requires O(n log n) time for sorting the points, and O(n) time to select an appropriate subset.Generating Permutations
A permutation can be obtained by selecting an element in the given set and recursively permuting the remaining elements.
Transpose of a Matrix
Transpose A Matrix
#include <conio.h>
int main()
{
int m, n, i, j;
int mat[10][10], trans[10][10];
printf(" Enter the number of rows and columns of matrix ");
scanf(" %d %d ", &m, &n);
printf(" Enter the elements of matrix \n ");
for( i = 0 ; i < m ; i++ )
{
for( j = 0 ; j < n ; j++ )
{
scanf(" %d ", &mat[i][j] );
}
}
for( i = 0 ; i < m ; i++ )
{
for( j = 0 ; j < n ; j++ )
{
trans[j][i] = mat[i][j];
}
}
printf(" Transpose of entered matrix :-\n ");
for( i = 0 ; i < n ; i++ )
{
for( j = 0 ; j < m ; j++ )
{
printf(" %d\t ", trans[i][j] );
}
printf(" \n ");
}
getch();
return 0;
}
Swap two Numbers
Swap Two Number
int main()
{
int x, y, temp;
printf("Enter the value of x and y\n");
scanf("%d", &x, &y);
printf("Before Swapping\n x = %d\ny = %d\n",x,y);
temp = x;
x = y;
y = temp;
printf("After Swapping\n x = %d\ny = %d\n",x,y);
return 0;
}
Swap String
Swap String
#include<string.h>
#include<malloc.h>
#include<conio.h>
main()
{
char first[100], second[100], *temp;
printf("Enter the first string ");
gets(first);
printf("Enter the second string ");
gets(second);
printf("\nBefore Swapping\n");
printf("First string: %s\n",first);
printf("Second string: %s\n\n",second);
temp = (char*)malloc(100);
strcpy(temp,first);
strcpy(first,second);
strcpy(second,temp);
printf("After Swapping\n");
printf("First string: %s\n",first);
printf("Second string: %s\n",second);
getch();
return 0;
}
Strong Number
Strong Number
{
int num,i,p,r,sum=0,save_num;
printf("\n Enter a number");
scanf("%d",&num);
save_num=num;
while(num)
{
i=1,p=1;
r=num%10;
while(i<=r)
{
p=p*i;
i++;
} //while
sum=sum+p;
num=num/10;
} //while
if(sum==save_num)
printf("%d is a Strong number", save_num);
else
printf("%d is not a Strong number", save_num);
}
Sort a Given Number of String
Sort A Given Number Of Strings
#include <conio.h>
#include <string.h>
main()
{
char str[4][10];
int i;
clrscr();
for( i = 0; i < 4; i++ )
{
printf(“ \nEnter name %d: ”, i+1 );
scanf(“ %s ”, str[i] );
}
printf(“\n Original Order\n”);
for(i = 0; i < 4; i++ )
printf(“ %s\t ”, str[i] );
for(i = 0; i < 4; i++ )
{
for(j = i + 1; j < 4; j++ )
if( strcmp(str[i], str[j]) > 0 )
{
strcpy( temp, str[i] );
strcpy( temp, str[i], str[j] );
strcpy( str[j], temp );
}
}
printf(“\n Sorted Order\n”);
for( i = 0; i < 4; i++ )
printf(“ %s\t ”, str[i]);
getch();
}
Subscribe to:
Posts (Atom)